Dew point
The dew point is the temperature to which a given parcel of humid air must be cooled, at constant barometric pressure, for water vapor to condense into liquid water. The condensed water is called dew when it forms on a solid surface. The dew point is a saturation temperature.
The dew point is associated with relative humidity. A high relative humidity indicates that the dew point is closer to the current air temperature. Relative humidity of 100% indicates the dew point is equal to the current temperature and the air is maximally saturated with water. When the dew point remains constant and temperature increases, relative humidity will decrease.[1]
The dew point is an important statistic for general aviation pilots, as it is used to calculate the likelihood of carburetor icing and fog, and to estimate the height of the cloud base.
At a given temperature but independent of barometric pressure, the dew point is a consequence of the absolute humidity, the mass of water per unit volume of air. If both the temperature and pressure rise, however, the dew point will rise and the relative humidity will lower accordingly. Reducing the absolute humidity without changing other variables will bring the dew point back down to its initial value. In the same way, increasing the absolute humidity after a temperature drop brings the dew point back down to its initial level. If the temperature rises in conditions of constant pressure, then the dew point will remain constant but the relative humidity will drop. For this reason, the same relative humidity on a day when it's 80°F, and on a day when it's 100°F will imply that a higher fraction of the air on the hotter day consists of water vapor than on the cooler day, i.e., the dew point is higher.
At a given barometric pressure but independent of temperature, the dew point indicates the mole fraction of water vapor in the air, or, put differently, determines the specific humidity of the air. If the pressure rises without changing this mole fraction, the dew point will rise accordingly; Reducing the mole fraction, i.e., making the air less humid, would bring the dew point back down to its initial value. In the same way, increasing the mole fraction after a pressure drop brings the relative humidity back up to its initial level. Considering New York (33 ft elevation) and Denver (5,130 ft elevation), for example, this means that if the dew point and temperature in both cities are the same, then the mass of water vapor per cubic meter of air will be the same, but the mole fraction of water vapor in the air will be greater in Denver.
Contents |
Relationship to human comfort
When the air temperature is high, the body's thermoregulation uses evaporation of perspiration (sweat) to cool down, with the cooling effect directly related to how fast the perspiration evaporates. The rate at which perspiration can evaporate depends on how much moisture is in the air and how much moisture the air can hold. If the air is already saturated with moisture, perspiration will not evaporate. The body's cooling system will produce perspiration in an effort to keep the body at its normal temperature even when the rate it is producing sweat exceeds the evaporation rate. So even without generating additional body heat by exercising, one can become coated with sweat on humid days. It is the unevaporated sweat that tends to make one feel uncomfortable in humid weather.
The air that affects comfort is not the air where the thermometer and humidity meters are located. It is the air that is touching one's body. As that portion of air is warmed by body heat, it will rise and be replaced with other air. If air is moved away from one's body with a natural breeze or a fan, sweat will evaporate faster, making perspiration more effective at cooling the body. The more unevaporated perspiration, the greater the discomfort.
A wet bulb thermometer also uses evaporative cooling, so it provides a good analog for use in evaluating comfort level.
Discomfort also exists when the dew point is low (below around −30 °C (−22 °F)). The drier air can cause skin to crack and become irritated more easily. It will also dry out the respiratory paths. OSHA recommends indoor air be maintained at 68 to 76°F (20 to 24.5°C) with a 20-60% relative humidity (a dew point of 24 to 60°F).[2]
Lower dew points, less than 10 °C (50 °F), correlate with lower ambient temperatures and the body requires less cooling. A lower dew point can go along with a high temperature only at extremely low relative humidity (see graph below), allowing for relative effective cooling.
Those accustomed to continental climates often begin to feel uncomfortable when the dew point reaches between 15 and 20 °C (59 and 68 °F). Most inhabitants of these areas will consider dew points above 21 °C (70 °F) oppressive.
| Dew point °C | Dew point °F | Human perception[1] | Rel. humidity at 32 °C (90 °F) |
|---|---|---|---|
| > Higher than 26 °C | > Higher than 80 °F | Severely high. Even deadly for asthma related illnesses | 65% and higher |
| 24–26 °C | 75–80 °F | Extremely uncomfortable, fairly oppressive | 62% |
| 21–24 °C | 70–74 °F | Very humid, quite uncomfortable | 52–60% |
| 18–21 °C | 65–69 °F | Somewhat uncomfortable for most people at upper edge | 44–52% |
| 16–18 °C | 60–64 °F | OK for most, but all perceive the humidity at upper edge | 37–46% |
| 13–16 °C | 55–59 °F | Comfortable | 38–41% |
| 10–12 °C | 50–54 °F | Very comfortable | 31–37% |
| < 10 °C | < 49 °F | A bit dry for some | 30% |
Measurement
Devices called dew point meters are used to measure dew point over a wide range of temperatures. These devices consist of a polished metal mirror which is cooled as air is passed over it. The temperature at which dew forms is, by definition, the dew point. Manual devices of this sort can be used to calibrate other types of humidity sensors, and automatic sensors may be used in a control loop with a humidifier or dehumidifier to control the dew point of the air in a building or in a smaller space for a manufacturing process.
Calculating the dew point
A well-known approximation used to calculate the dew point Td given the relative humidity RH in percent and the actual temperature T of air is:
where
where the temperatures are in degrees Celsius and "ln" refers to the natural logarithm. The constants are:
- a = 17.271
- b = 237.7 °C
This expression is based on the August–Roche–Magnus approximation for the saturation vapor pressure of water in air as a function of temperature.[3] It is considered valid for
- 0 °C < T < 60 °C
- 1% < RH < 100%
- 0 °C < Td < 50 °C
Simple approximation
There is also a very simple approximation that allows conversion between the dew point, the dry-bulb temperature and the relative humidity. This approach will be accurate to within about ±1 °C as long as the relative humidity is above 50%.
The equation is:
or
This can be expressed as a simple rule of thumb:
For every 1 °C difference in the dew point and dry bulb temperatures, the relative humidity decreases by 5%, starting with RH = 100% when the dew point equals the dry bulb temperature.
where in this case RH is in percent, and T and Td are in degrees Celsius.
The derivation of this approach, a discussion of its accuracy, comparisons to other approximations, and more information on the history and applications of the dew point are given in the Bulletin of the American Meteorological Society.[4]
For temperatures in degrees Fahrenheit,
or
For example, a relative humidity of 100% means dew point is the same as air temp. For 90% RH, dew point is 3 degrees Fahrenheit lower than air temp. For every 10 percent lower, dew point drops 3 °F.
Closer approximation
A calculation used by NOAA is:[5]
where:
- RH is relative humidity in percentage and
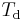 is dew point in degrees Celsius
is dew point in degrees Celsius  and
and 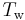 are the dry-bulb and wet-bulb temperatures respectively in degrees Celsius
are the dry-bulb and wet-bulb temperatures respectively in degrees Celsius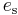 is the saturated water vapor pressure, in units of millibar, at the dry-bulb temperature
is the saturated water vapor pressure, in units of millibar, at the dry-bulb temperature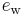 is the saturated water vapor pressure, in units of millibar, at the wet-bulb temperature
is the saturated water vapor pressure, in units of millibar, at the wet-bulb temperature is the actual water vapor pressure, in units of millibar
is the actual water vapor pressure, in units of millibar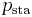 is "station pressure" (absolute barometric pressure at the site that humidity is being calculated for) in units of millibar (which is also hPa).
is "station pressure" (absolute barometric pressure at the site that humidity is being calculated for) in units of millibar (which is also hPa).
For greater accuracy use the Arden Buck equation to find the water vapor pressures.
Frost point
The frost point is similar to the dew point, in that it is the temperature to which a given parcel of humid air must be cooled, at constant barometric pressure, for water vapor to be deposited on a surface as ice without going through the liquid phase. (Compare with sublimation.) The frost point for a given parcel of air is always higher than the dew point, as the stronger bonding between water molecules on the surface of ice requires more temperature to break.[6]
See also
References
- ^ a b Horstmeyer, Steve (2006-08-15). "Relative Humidity....Relative to What? The Dew Point Temperature...a better approach". Steve Horstmeyer, Meteorologist, WKRC TV, Cincinnati, Ohio, USA. http://www.shorstmeyer.com/wxfaqs/humidity/humidity.html. Retrieved 2009-08-20.
- ^ http://www.osha.gov/pls/oshaweb/owadisp.show_document?p_table=INTERPRETATIONS&p_id=24602
- ^ "MET4 AND MET4A CALCULATION OF DEW POINT". Paroscientific, Inc. 4500 148th Ave. N.E. Redmond, WA 98052. 2007-09-13. http://www.paroscientific.com/dewpoint.htm.
- ^ M. G. Lawrence, "The relationship between relative humidity and the dew point temperature in moist air: A simple conversion and applications", Bull. Am. Meteorol. Soc., 86, 225–233, 2005
- ^ http://www.srh.noaa.gov/images/epz/wxcalc/rhTdFromWetBulb.pdf
- ^ Haby, Jeff. "Frost point and dew point". http://www.theweatherprediction.com/habyhints/347/. Retrieved September 30, 2011.
External links
- What is the dew point?
- Dew point definition NOAA Glossary
- Dew point formula
- Often Needed Answers about Temp, Humidity & Dew Point from the sci.geo.meteorology
- Humidity calculator
- Dew point calculator in construction
|
|||||||||||||||||
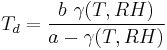
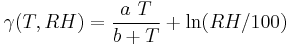
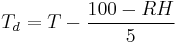

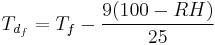
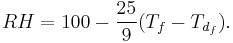
![\begin{align}
e_\text{s} & = 6.112 \exp \left( {17.67T \over T%2B243.5} \right) \\[8pt]
e_\text{w} & = 6.112 \exp \left( {17.67T_\text{w} \over T_\text{w} %2B 243.5} \right) \\[8pt]
e & = e_\text{w} - p_\text{sta} \left(T-T_\text{w}\right) 0.00066 \left[1 %2B (0.00115 T_\text{w}) \right] \\[8pt]
RH & = 100 {e \over e_\text{s}} \\[8pt]
T_\text{d} & = {243.5 \ln(e/6.112) \over 17.67 - \ln(e/6.112)}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/255a8576cc9f221af4c30a130539e22e.png)